泡沫金属相变材料熔化传热过程的数值分析

1引 言

随着能源危机的日益加剧, 利用相变材料存储能量已成为研究热点, 虽然相变材料本身具有储热密度大, 且储能过程近似恒温等优点, 但这类材料的热传导率却很低, 在一定程度上限制了它的应用。为了提高相变材料的导热能力, 可通过在相变材料中添加各种形态的金属、石墨、肋片等措施, 来强化相变材料的导热系数。为此, 国内外学者做了大量理论和实验方面的研究^{[ 1 5]} 。彭冬华等^{[ 6]} 利用泡沫铝为骨架, 考虑金属骨架与流体之间的不同的传热特性, 建立了泡沫金属内熔化相变传热的双温度模型。Bedecarrats 等^{[ 7]} 对填充有球形相变材料的蓄热槽内部的相变传热特性做了数值分析。郭茶秀等^{[ 8]} 利用计算流体力学软件 FLUENT 凝固/ 熔化模型对一种相变材料蓄冷球的凝固过程进行数值模拟研究。Mesalhy 等^{[ 9]} 研究了将具有各种不同导热系数和不同孔隙率的多孔金属基体加入相变材料, 对相变蓄热装置热性能的影响, 并采用数值方法对水平圆柱环的熔化过程进行了研究。

综上所述, 采用泡沫金属作为金属骨架能改善相变材料的传热性能。本文采用近年来开发的孔隙率为 90% 的泡沫金属铝为骨架, 孔隙中填充石蜡作为储能介质, 采用数值方法, 利用 FLU EN T 软件对蓄热球相变传热过程进行分析研究。

2       数学模型的建立

图1 所示为相变蓄热装置示意图, 蓄热球在密闭式圆柱形槽中有规则的堆放, 载热流体从蓄热槽孔隙流过球形蓄热体表面, 蓄热球吸收载热体携带的热量, 从而由球壁向球内逐渐熔化, 直至整个球内完全发生相变。蓄热球的物理模型如图 2 所示。由于与整个储能槽相比, 蓄热球直径较小, 故单个蓄热球周围载热流体温度可视为同一值。

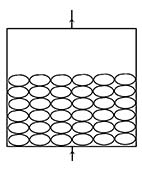
图1相变蓄热球储能槽示意图

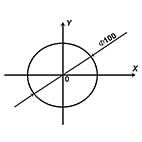
图2 蓄热球物理模型

为分析方便, 对物理模型作如下假设: ( 1) 假设载热流体流动为层流, 且流体和固体处于局部热平衡; ( 2) 初始时刻球内蓄热介质的温度均匀一致; ( 3) 石蜡相变范围在 332~ 334K 之间; ( 4) 物性参数在每相中不随温度变化, 在处于熔融状态时, 参数随温度线性变化; ( 5) 由于导热系数对传热的影响较大, 故加入泡沫金属后, 忽略其它物性参数变化的影响。

材料的物性

Tanle 1Material properties

本文言中加入泡沫金属后采用有效导热系数进行下一步的传热计算。其有效导热系数计算公式取值：

其中：Km为泡沫金属的导热系数，J/（kg  K）；Kr为石蜡的当量导热系数：为泡沫金属的孔隙率.

根据 FTU　EN　T　的融化／凝固的基本理论，并采用以上假设后，数学模型可以简化为连续性方程：

（u）+（v）=0

  X     y

其中, cs, l 为固、液态石蜡比热容, J/ kg K; ks, l 为固、液态石蜡导热系数,J/ kg K; T m为石蜡发生相变的平均温度, K; !为液态石蜡的动力粘度, kg/ ( m s) ; H m 为石蜡的相变焓, J。

3       FLU ENT 的分析及数值模拟结果

3. 1    几何模型及网格划分

本文对直径为 100mm 的蓄热球进行模拟, 球壁面为固壁边界。利用 FLUENT 自带的前处理软件

 Gambit 进行建模和网格划分。在 Gam bit 2. 2. 30 的 Mesh 模块中选用四边形单元, 蓄热球划分的计算网格如图 3 所示。

 3. 2  计算参数的设置

在 FLUENT 6. 2. 16 软件中, 选择 2D 分离式、非稳态求解器求解, 流动为层流, Solidification/ Melting模型模拟蓄热球的相变传热过程。按表 1 所示数据输入相变材料的各热物性参数。设置残差值为 1e 06, 蓄热时初始化温度定为 35 , 固壁温度 65 。单纯的相变材料蓄热球时间步长选为 10~ 30s, 加入泡沫金属的步长定为 0. 5 ~ 2s。放热时初始化温度定为 65 , 固壁温度为 35 , 单纯的相变材料蓄热球时间步长选为 10~ 30s, 加入泡沫金属的步长定为 0. 5~ 2s。

图3 蓄热球网格划分

3. 3    模拟结果及分析

现对初始温度为 308K, 固壁温度为 338K 的蓄热球蓄热过程进行模拟分析, 图 4 为无泡沫金属纯石蜡熔化时间 t = 1000s 时的温度分布图, 图 5 为有泡沫金属石蜡熔化时间 t = 1000s时的温度分布图。从这两图可以看出球内温度场是由外层向内层逐步变化的,从图 4 中石蜡的温度分布可知, 由于纯石蜡的热导率低, 故传热进行得比较慢。在 1000s 时, 球内中心点温度仅为 311K, 球内温差高达 27 , 而图 5 中加入泡沫金属的石蜡在 1000s 时刻, 蓄热球中心点温度已经到达了 332K, 球内温差仅为 6 。

图 4  无泡沫金属石蜡 1000s 的温度分布图

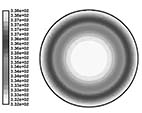
图 5  泡沫金属石蜡 1000s 时的温度分布图

 6 为无泡沫金属纯石蜡熔化时间 t = 1000s 时蓄热球内的固相液相分布比例, 图 7 为有泡沫金属石蜡熔化时间 t = 1000s 时蓄热球内的固相液相分布比例。比较两图可以发现, 无泡沫金属的蓄热球经过 1000s 后, 球内相变材料基本处于未熔化状态, 而填充

泡沫金属的蓄热球已经开始熔化。

图 8 为无泡沫金属纯石蜡熔化时间 t = 3000s 时的温度分布图, 图 9 为有泡沫金属石蜡熔化时间 t = 3000s 时的温度分布图。由图可知, 随着熔化时间的进行, 无泡沫金属石蜡球内中心点温度已经达到了324K, 球内温差由 1000s 时刻的 27 减小到了 14 的状态。

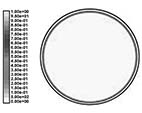
图 6  无泡沫金属石蜡 1000s 固液相比例

图 7  有泡沫金属石蜡 1000s 固液相比例

而有泡沫金属的石蜡球在 3000s 时刻, 蓄热球中心点温度已经到达了 338K, 球内整体温度基本处于热平衡

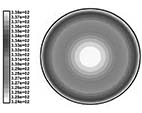
图 8  无泡沫金属纯石蜡 3000s 温度分布图

图 10 为无泡沫金属纯石蜡熔化时间 t = 3000s 时蓄热球内的固相液相分布比例, 图 11 为有泡沫金属石蜡熔化时间 t = 3000s 时蓄热球内的固相液相分布比例。由两图可以看出, 随着熔化时间的进行, 在 t = 3000s 时刻, 球内相界面的位置变化以及球内熔化区域逐渐增加, 液相比例逐步减小, 同时也可以发现, 相界面是沿着球径由外向内逐层推进的。比较两图可以发现, 3000s 时刻, 在无泡沫金属蓄热球刚刚处于熔化开始阶段时, 有泡沫金属的蓄热球内相变材料已经达到了完全融化的状态。

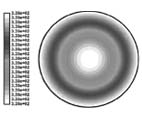
图 9  有泡沫金属石蜡 3000s 的温度分布图

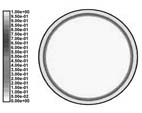
图 10  无泡沫金属石蜡 3000s 固液相比例

图 11  有泡沫金属石蜡 3000s 固液相比例

4     结 论

( 1) 通过对泡沫金属蓄热球与未加入泡沫金属蓄热球相变传热过程的数值模拟的比较分析, 研究了泡沫金属对蓄热球内相变熔化过程的影响。结果表明, 多孔泡沫金属对蓄热球内流体相变传热过程具有重要的影响, 填充泡沫金属的相变材料蓄热球能显著缩短其蓄热时间, 提高蓄热装置的蓄热速率, 从而改善相变储能装置的传热性能和内部温度均匀性, 对相变问题的数值模拟以及相变蓄能装置的设计具有重要的参考价值。

( 2) 通过与文献[ 8] 所述的计算结果比较, 验证了模型的正确性。

( 3) 通过计算分析, 可知热媒体入口流量、入口温度等因素对蓄热球相变熔化过程起着重要作用, 由此构建更合理的相变材料储能槽, 以提高蓄热槽的蓄放热效率。